We need more data!

In the recent years we have seen a increase on focusing on bias in Machine Learning. This is not the classical variance vs. bias concept. Is rather the social context of bias, which leads to profiling and systematic racism. Since ML algorithms are applied on every level now, this has the repercussion that some of those processes will discriminate against a minority. The European Union presented drafts that go in much more detail explaining the role of accountability of automated decision making in AI. However, these guidelines do not describe specifically how to make your model have less bias towards a group.

A couple days ago a friend suggested me a talk of Vincent Warmerdam. I loved the whole talk and was a bit curios on one trick that he mentions there about information filtering. I will go about and explain the trick as I really liked the mathematics behind it.

The trick

This trick basically is orthogonalizing of vectors to remove influence that a lot of ML algorithms pick up (i.e. correlation). The process is simple in the sense that it could be expressed in few lines as:

1
2
3
4
5
6
7
8
9
10
11
def filter_information(vectors):    
    if np.linalg.matrix_rank(vectors.T) != vectors.shape[0]:
        raise Exception("Careful, some sort of linear dependence!")
     
    q, r = np.linalg.qr(vectors.T)
    q = q.T * -1 # make sure the vectors are pointing at the right direction
    norm_factor = np.linalg.norm(vectors, axis=1)
    
    filtered = (q.T * norm_factor).T
    
    return filtered

The algorithm contains some linear algebra, especially the QR decomposition which can be summarized as decomposing \(A = QR\), where \(Q\) is an orthonormal matrix (i.e. each column is orthogonal and normalized to every other column), and \(R\) is an upper-triangular matrix. We are after the \(Q\) matrix, because that is exactly what we need. If we have 2 vectors which satisfy \(v_1 \cdot v_2 \neq 0\) (i.e. not orthogonal), the decomposition moves one of the vectors to form a \(90^{\circ}\) angle, thus making the dot product equal to \(0\). We need to take into account that this decomposition also normalizes the vectors by dividing by their magnitude \(||v_i||\). If we multiply each orthonormal vector with their respective norm, we get the orthogonalized vectors back. This is what we want! Put more into visuals:

1
2
3
4
5
6
7
8
9
10
vectors = np.array([
    [2, 0, 3], # v0
    [2, 3, 1], # v1
])

ortho = filter_information(vectors)

# result:
# array([[ 2.        ,  0.        ,  3.        ],
#       [ 1.07981105,  3.50938591, -0.71987403]])

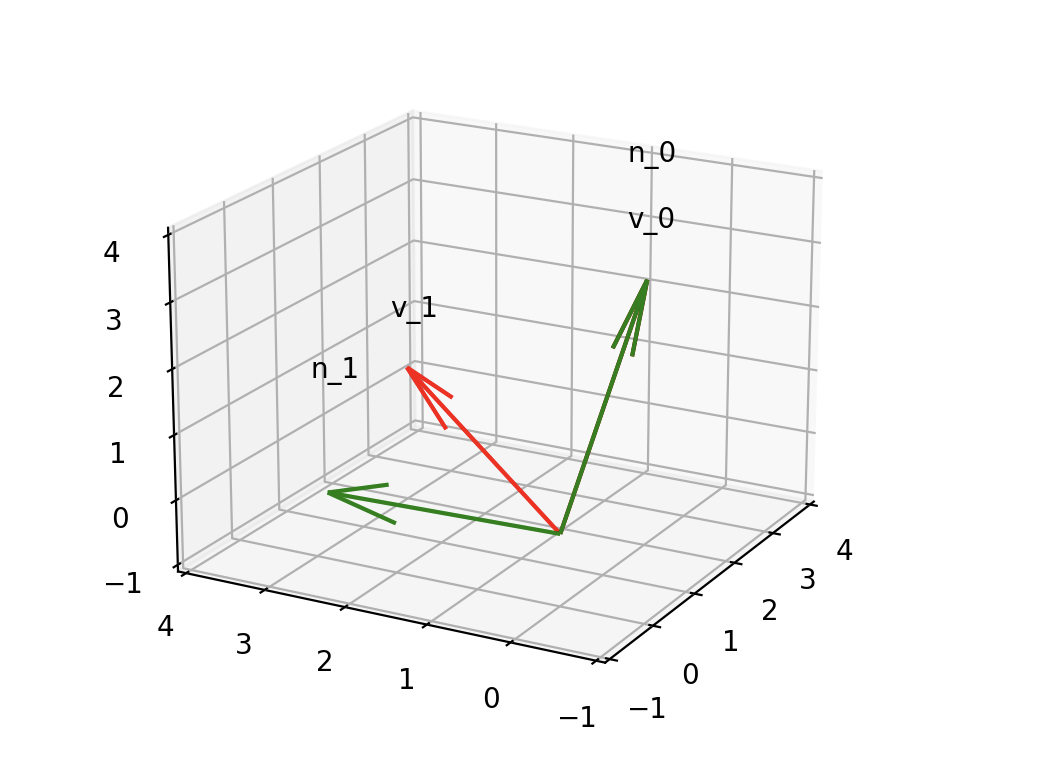
The vector \(v_0\) and \(v_1\) (red) were not orthogonal before, but after the filter information call, the result is orthogonal (green). This is a good trick to make sure no information spills from a vector that is considered sensitive. However, as all good things in life, this method also has a couple of downsides. It looks to good to be true.

Downsides

The elephant in the room here is that you are changing your data. This is usually a “no-no!” kind of situation given input (i.e. ground truth) data. This may make your algorithm to be more fair, as Vincent explains in his talk, but the problem is that you loose much more in the process that you get out of it. In simple words, you loose the interpretability of your input columns. For example: having “age” be \(-12.7443\) does not go well with management, or with anyone really. And trying to explain that you need to store a transformation matrix \(M\) for each row of your data, to inverse the operation; sorry, you lost almost anyone in the room. And the final blow, many companies are measure oriented in terms of model testing, which means they will promote the best performing model to the holy production. And this kind of model will not be performing that good, as we are doing some kind of implicit “dimensionality” reduction that is fairer, but comes with looser definition of arriving at a decision. I totally agree with Vincent when he mentions that sometimes we do not need to make a automatic decision. However, the current state of our community is that we have too.

Conclusion

All said, I really do not want to pick on the downsides of a method as this was promised to be just a trick, rather than a systematic way to combat social bias. I really love the simplicity of this method, and what it implies. It makes you think more about the way we have been cooking a big stew of bias and discrimination in our models. Any talk that achieves that for me is a very successful talk. And another cool thing about this method is that it can be used for other things that what we described here, its still a valid orthogonalization of vectors method. Rename it to ortho_vec and use it in computational geometry instead, if need rises.