One of the most common types of data sources is timeseries or geometric data, such as 2D GPS sensor data. However, these data often contain noise and require preprocessing to enhance interpretability. In this post, we will explore a simple yet powerful algorithm designed to simplify line segments in timeseries or vector paths. This algorithm is particularly useful when dealing with noisy or high-resolution data, allowing for a reduction in data points while preserving the overall fidelity.
The Ramer-Douglas-Peucker Algorithm
The Ramer-Douglas-Peucker algorithm, commonly abbreviated as rdp, is a widely used method for line simplification. It operates by taking a single argument, epsilon, which represents the maximum distance used to filter out unnecessary points along the path. By applying the algorithm, we can determine which points to retain and which to remove, effectively simplifying the path.
To better understand how the algorithm works, you can refer to the animation provided in the Wikipedia article on the Ramer-Douglas-Peucker algorithm. The animation demonstrates how the algorithm makes decisions regarding the retention or removal of points within a given path.
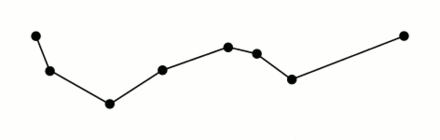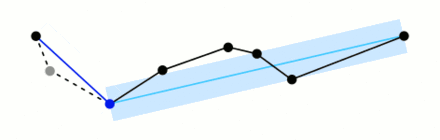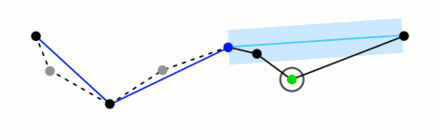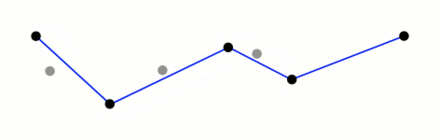
There is a small useful implementation in python of this method and you can find it here (also the docs).